Олимпиадная задача Канеля-Белова: произведение выражений с корнями — целое ли это квадрат?

  Лемма. Если число a₀ целое, а числа a₁, ..., a_n натуральные, то произведение всех 2ⁿ выражений вида 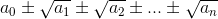    – целое число.

  Доказательство. Рассмотрим выражение P, полученное перемножением 2ⁿ сумм вида  a₀ ± x₁ ± x₂ ± ... ± x_n.  Раскрывая скобки и приводя подобные, получим многочлен от переменных x₁, x₂, ..., x_n с целыми коэффициентами. Результат, очевидно, не зависит от того, как мы группируем скобки и в каком порядке их перемножаем. Разобьём, например, все произведение на 2^n–1 сомножителей вида

  (S = ± x₂ ± x₃ ± ... ± x_n  с какими-то фиксированными знаками). В первое слагаемое x₁ вообще не входит, а во второе – входит в чётной степени. Поэтому и после раскрытия скобок в произведении таких выражений x₁ входит в каждый одночлен в чётной степени. В силу симметрии то же верно для каждого из остальных x_i. Подставляя теперь 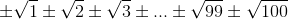    (i = 1, ..., n)  в многочлен, мы получим сумму произведений целых чисел (корни в чётных степенях дают целые), то есть целое число.   а) Применив лемму к числам  a₀ = 0,  a₁ = 1,  ...,  a₁₀₀ = 100,  сразу получим требуемый результат.   б) Применив лемму к числам  a₀ = 1,  a₁ = 2,  ...,  a₉₉ = 100,  получим, что произведение P всех 2⁹⁹ выражений вида  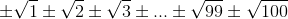   – целое число. Но оставшиеся 2⁹⁹ сомножителей – это те же самые числа, взятые с противоположным знаком. Поэтому их произведение равно  (–1)²⁹⁹P = P,  а произведение всех 2¹⁰⁰ сомножителей равно P².

Ответ задачи отсутствует