Олимпиадная задача по планиметрии: разбиение многоугольника ломаной и отрезком, 10–11 класс

  а) Вот пример:

  Докажем, что шестиугольник на рисунке нельзя разбить отрезком на два равных многоугольника. Действительно, такой разрез должен пройти через вершинуB(иначе в одном многоугольнике будет угол, больший развёрнутого, а в другом – нет). Но единственный разрез, проведённый через точкуB, который делит наш шестиугольник на два многоугольника с одинаковым числом сторон, – это разрез по отрезкуAB(в остальных случаях одна из частей – треугольник или четырёхугольник, а вторая – пяти- или шестиугольник). А отрезокABразбивает шестиугольник на прямоугольник и параллелограмм, прямоугольником не являющийся.   См. также пример в п. б).   б) Приведём контрпример. На рисунке слева изображён пятиугольник, полученный из прямоугольника 2×3 отрезанием двух равных прямоугольных треугольников с катетами 1 и 2. Он разрезан ломаной на два равных шестиугольника. Но разбить его на два равных многоугольника отрезком нельзя.   Действительно, такой разрез должен пройти через какую-то вершину и разбить на две части противоположную ей сторону (иначе получатся многоугольники сразнымчислом сторон). Кроме того, наборы длин сторон частей должны быть одинаковы. У исходного пятиугольника есть парадлинныхи паракороткихсторон, а также однасредняя. Разрез не может разбить ни длинную, ни короткую стороны – тогда исчезнет пара. Единственная возможность – разбить пополам среднюю сторону. Но тогда одна из частей – параллелограмм, а другая – нет (см. рис. справа).   в) Пусть многоугольник M разбивается некоторой ломаной A₁...A_n на части P и Q и движение Ф (поворот или перенос) переводит P в Q. Рассмотрим вершину A₂. Она является вершиной двух углов, один из которых – внутренний угол многоугольника P, а второй – внутренний угол многоугольника Q. Поскольку точка A₂ лежит внутри M, один из этих углов (пусть угол многоугольника P) больше 180°. Движение Ф совмещает этот угол с одним из углов многоугольника Q, вершина которого также должна лежать внутри M (у выпуклого многоугольника M все углы меньше 180°). Поэтому она совпадает с одной из вершин нашей ломаной:  Ф(A₂) = A_k.

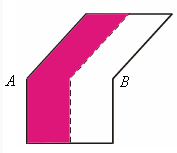
  Заметим, что при обходе границ многоугольников P и Q против часовой стрелки вершины ломаной проходятся в противоположных порядках (если вдоль границы P мы идём от A₁ к A₂, ..., A_n, то вдоль границы Q – от A_n к A₁). С другой стороны, направление обхода границы P от A₁ к A₂, ..., A_n совпадает с направлением обхода границы Q от Ф(A₁) к Ф(A₂), ..., Ф(A_n). Следовательно, Ф переводит A₃ в A_k–1, A₄ в A_k–2 и т.д. Поэтому найдётся либо такой номер i, что  Ф(A_i) = A_i  (если k чётно), либо такой номер i, что  Ф(A_i) = A_i+1  и  Ф(A_i+1) = A_i  (если k нечётно). Первый случай невозможен: прилегающие к вершине A_i углы многоугольников P и Q не равны.

  Во втором случае движение Ф "переворачивает" отрезок A_iA_i+1, следовательно, Ф – центральная симметрия (поворот на 180°) относительно середины этого отрезка. Поэтому многоугольник M центрально симметричен. Но тогда любая прямая, проведённая через его центр симметрии, делит M на два равных многоугольника.

Утверждения а) и б) неверны, утверждение в) верно.