Олимпиадная задача Фомина: неравенства путей на графах круглого острова, 9–11 класс

  Введём на каждом пути порядок прохождения портов и развилок.

  а) Рассмотрим всевозможные пары путей, идущих из порта 1 в порт 3 и из 2 – в 4 (рис. 1); коротко будем писать: пары  1 → 3,  2 → 4.  Их число равно  f₁₃f₂₄.  На каждой такой паре есть хоть одна общая точка (развилка или порт). Выберем среди них точку M пути  1 → 3,  ближайшую к порту 1, и поменяем "хвосты" путей, начиная от этой точки M. Так мы получим некоторую пару путей  1 → 4,  2 → 3.  Ясно, что разным парам путей  1 → 3,  2 → 4  при этом соответствуют разные пары  1 → 4,  2 → 3,  поскольку точка M и операция замены "хвостов" определены однозначно. (Более того, ясно, что любая пара

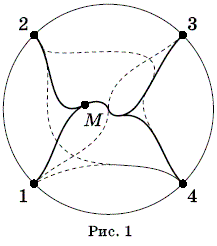
1 → 4,  2 → 3,  имеющая хоть одну общую точку, будет соответствовать некоторой паре  1 → 3,  2 → 4.)

  Отсюда следует неравенство  f₁₄f₂₃ ≥ f₁₃f₂₄,  поскольку левая часть – это общее число пар путей  1 → 4,  2 → 3  (более точное утверждение: разность

f₁₄f₂₃ – f₁₃f₂₄  равна числу пар путей  1 → 4,  2 → 3,  не имеющих общих точек).   б) Среди шести отображений множества  {1, 2, 3}  на  {4, 5, 6}  назовём чётными те, для которых отображение "сохраняет ориентацию треугольника"

(1 → 4, 2 → 5, 3 → 6;  1 → 5, 2 → 6, 3 → 4  и  1 → 6, 2 → 4, 3 → 5,  и нечётными – остальные. Если поменять местами образы каких-то двух из номеров 1, 2, 3, то чётность меняется на противоположную.

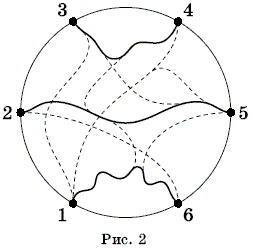
  Рассмотрим тройку путей  1 → i,  2 → j,  3 → k,  где  (i, j, k) – некоторая перестановка  (4, 5, 6).  Если какие-то два из них имеют хоть одну общую точку, то выберем самую раннюю из них M (ближайшую к порту 1 на пути  1 → i  или, если  1 → i  не пересекается с двумя другими путями, ближайшую к порту 2 на пути  2 → j)  и поменяем "хвосты" двух путей, проходящих через эту точку. (Если через M проходят все три пути  1 → i,  2 → j,  3 → k,  то меняем хвосты  1 → i  и  2 → j.)  Заметим, что чётность тройки при перемене хвостов меняется. Таким образом, имеется взаимно однозначное соответствие между чётными и нечётными тройками путей, имеющих точки пересечения. Каждая тройка не имеющих общих точек путей имеет вид  1 → 6,  2 → 5,  3 → 4  (рис. 2), то есть нечётна. Значит, нечётных троек не меньше. Отсюда следует требуемое неравенство.

Ответ задачи отсутствует