Восстановление координат и осей по параболе y = x² — олимпиадная задача по планиметрии

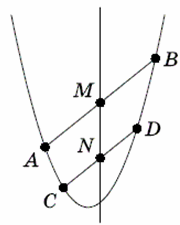
  Докажем следующую лемму.   Лемма. Пусть M и N – середины двух параллельных хорд параболы. Тогда прямая MN параллельна оси параболы (рис. 1).

 Доказательство. Пусть хордыABиCDпараболы лежат на параллельных прямых  y = kx + a  и  y = kx + b,  тогда абсциссы точек  A, B, C, D  – это корни уравнений  x² =kx + a  и  x² =kx + b,  а абсциссы точекMиN– полусуммы корней этих уравнений, то есть по теореме Виета равны^k/₂.  Следовательно, прямаяMNпараллельна осиOy.   Вернёмся к решению задачи. Проводим последовательно две параллельные хорды параболы; прямую, проходящую через их середины (параллельную Oy); перпендикуляр к этой прямой, пересекающий параболу в двух точках; серединный перпендикуляр к полученной хорде. Этот перпендикуляр и будет осью Oy, а ось Ox – это перпендикуляр к Oy в точке пересечения с параболой.

Ответ задачи отсутствует