Олимпиадная задача по планиметрии: равенство длин отрезков на сторонах ромба

Решение 1:   Пусть угол при вершине A ромба ABCD – не тупой. Обозначим длины красных, белых и синих отрезков (в порядке обхода  A → B → C → D → A)  r₁, w₁, b₁, r₂, ..., b₄.  Опустим из центра O окружности перпендикуляры OK, OL, OM и ON на стороны AB, BC, CD и DA соответственно (см. рис.).

  Эти перпендикуляры разделят белые отрезки пополам. Поэтому  AK = r₁+ ½w₁, KB = b₁+ ½w₁  и т. д. Теперь достаточно доказать, что AK + BL + CM + DN = KB + LC + MD + NA.    На самом деле, верны даже равенства  AK + CM = LC + NA  и  BL + DN = KB + MD.  Докажем, например, первое из них. Для этого опустим еще перпендикулярыCPиCQна прямыеABиAD. CP = CQ  в силу симметрии ромба относительно диагоналиAC.KPCM– параллелограмм (даже прямоугольник), значит,  KP = CM  и  AK + CM = AP.  Аналогично  LC + NA = AQ,  то есть  LC + NA = AQ = AP = AK + CM.

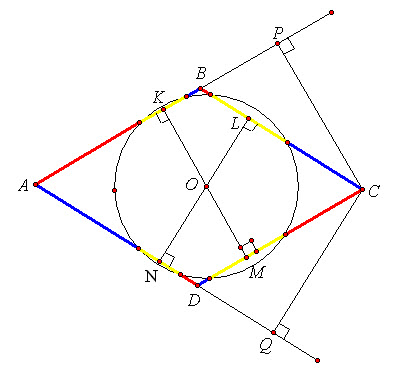
Решение 2:   Пусть d – длина стороны ромба. По теореме о секущей  r₁(d – b₁) = b₄(d – r₄),  r₂(d – b₂) = b₁(d – r₁),  и т. д. Сложив эти 4 соотношения, получим

(r₁ + r₂ + r₃ + r₄)d – (r₁b₁ + ... + r₄b₄) = (b₁ + ... + b₄)d – (r₁b₁ + ... + r₄b₄).  Следовательно,  r₁ + r₂ + r₃ + r₄ = b₁ + b₂ + b₃ + b₄.

Ответ задачи отсутствует