Олимпиадная задача по планиметрии для 10–11 классов: углы в равнобедренном треугольнике
Задача
В равнобедренном треугольнике ABC (AB = AC) угол A равен α. На стороне AB взята точка D так, что AD = AB/n. Найдите сумму n – 1 углов, под которыми виден отрезок AD из точек, делящих сторону BC на n равных частей:
а) при n = 3;
б) при произвольном n.
Решение
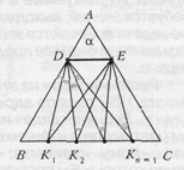
б) Построим на стороне AC = AB точку E, симметричную D относительно высоты, опущенной из A – оси симметрии треугольника ABC. Сумма углов, которую требуется найти, очевидно, в два раза меньше суммы ∠DK1E + ∠DK2E + ... + ∠DKn–1E (*)
углов, под которыми виден отрезок DE из точек K1, ..., Kn–1, делящих основание AC на n равных частей. Действительно, суммы углов, под которыми из этих точек видны отрезки AD и AE, равны, и ∠DKiA + ∠AKiE = ∠DKiE для каждого i = 1, 2, ..., n – 1. Но поскольку BDEK1, K1DEK2, K2DEK3, ..., Kn–1DEC – параллелограммы, сумму (*) легко "собрать" в один угол BDKn–1, равный ∠A = α (см. рисунок):
∠BDK1 = ∠DK1E, ∠K1DK2 = ∠DK2E, ..., ∠Kn–2DKn–1 = ∠DKn–1E.
Ответ
α/2.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь