Олимпиадная задача по планиметрии: квадраты на сторонах и вершинах треугольника (10–11 класс)
Задача
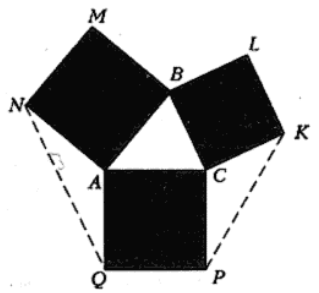
На сторонах треугольника ABC во внешнюю сторону построены квадраты ABMN, BCKL, ACPQ. На отрезках NQ и PK построены квадраты NQZT и PKXY. Разность площадей квадратов ABMN и BCKL равна d. Найдите разность площадей квадратов NQZT и PKXY
а) в случае, если угол ABC прямой,
б) в общем случае.
Решение
По теореме косинусов (см. рисунок) NQ² = AN² + AQ² – 2AN·AQ cos ∠NAQ = AB² + AC² + 2AB·BC cos ∠A,
BC² = AB² + AC² – 2AB·BC cos ∠A. Поэтому NQ² + BC² = 2AB² + 2AC².
Аналогично PK² + AB² = 2BC² + 2AC². Следовательно, NQ² – PK² = 3(AB² – BC²) = 3d.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет