Олимпиадная задача: образуем квадрат из шестизначного числа с припиской цифр

  а) Возьмём произвольное число, оканчивающееся нулями, квадрат которого – 12-значное число, начинающееся с 5, например  A = 750000

(A² = 5625·10⁸).  Поскольку  (A – 1)² = A² – 2A + 1,  предшествующий A² квадрат равен  562500000000 – 2·750000 + 1 = 562498500001.  Значит, 12-значного квадрата, начинающегося цифрами 562499, не существует.   б) Пусть A² – 12-значное число, начинающееся с 1, то есть  10¹¹ ≤ A² < 2·10¹¹.  Соседние квадраты отличаются от A² на  2A – 1  и  2A + 1,  а 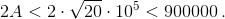    Поэтому разница между соседними квадратами меньше миллиона, так что в ряду последовательных квадратов между 10¹¹ и 2·10¹¹ встретятся числа, начинающиеся с каждого набора из шести цифр.   в) К любым n цифрам можно приписать еще  n + 1  цифру так, что полученное число из  2n + 1  цифры будет полным квадратом. Действительно, на участке от 10²ⁿ до 10²ⁿ⁺¹ разница между соседними квадратами не превосходит  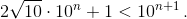   Докажем, что  k(n) ≥ n + 1.  Рассмотрим квадрат, предшествующий 10²ⁿ:     Таким образом, к числу 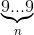    нельзя приписать n цифр так, чтобы получился квадрат. Ясно также, что к нему нельзя приписать  n – 2,  n – 4,  ... цифры: соответствующее число слишком близко к (10^n–1)², (10^n–2)², ... Поэтому  k(n) ≠ n  (а также &nbspn – 2,&nbsp n – 4,&nbsp ...).

  Рассмотрим ещё квадрат, предшествующий  (2·10^n–1)²: 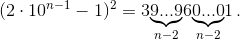    Таким образом, к числу  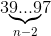   нельзя приписать  n – 1  (а также  n – 3,  n – 5,  ...) цифр, чтобы получился квадрат, поэтому  k(n) ≠ n – 1  (n – 3,  n – 5,  ...).

а) Не к любому;  б) к любому;  в)  k(n) = n + 1.