Олимпиадная задача по планиметрии и алгебраическим методам для 7–9 классов: максимальное число самопересечений у шестизвенной замкнутой ломаной

  а) На рисунке изображена шестизвенная ломаная с семью точками самопересечения.

  б) Докажем, что такая ломаная не может иметь больше семи самопересечений. Пусть общее число самопересечений равно N. Для каждого звена рассмотрим число точек самопересечения, которые лежат на этом звене, и обозначим через S сумму этих чисел. Тогда  S ≥ 2N  (если в одной точке пересекаются два звена, то эта точка входит в сумму дважды, если три или больше — больше двух раз). На каждом звене может лежать не больше трёх точек самопересечения, так как кроме этого звена и двух соседних с ним имеются всего три звена, которые могут с ним пересекаться. При этом три точки могут быть только на "диагональном" звене: таком, что из четырёх вершин, не являющихся его концами, две лежат в одной полуплоскости от него, а две другие – в другой. (Если по какую-то сторону от звена лежит лишь одна вершина, то нельзя провести больше двух отрезков к вершинам, лежащим по другую сторону звена.) Таких "диагональных" звеньев максимум три. На каждом из остальных лежат не больше чем по две точки самопересечения, поэтому  S ≤ 3· 2 + 3·3 = 15,  то есть  N ≤ ^S/₂ ≤ 7,5.

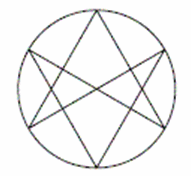
Ответ задачи отсутствует