Назад

Олимпиадная задача по планиметрии и комбинаторной геометрии для 8-9 классов: поиск равных семиугольников с несовпадающими сторонами

Задача 198279 • Сложность: 3 • 8-9 класс
Задача

а) Существуют ли два равных семиугольника, все вершины которых совпадают, но никакие стороны не совпадают?

б) А три таких семиугольника?

Решение

Пример строим так. Возьмём правильный треугольник ABC с центром O. Применим к треугольнику ABC гомотетию с центром в точке O и коэффициентом  k < 1,  повернём полученный треугольник на очень малый угол по часовой стрелке; полученный треугольник обозначим A'B'C' (см. рисунок).

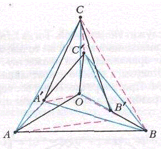
Первый семиугольник – замкнутая ломанаяAOC'A'CB'BA. Второй и третий семиугольники получаются из первого поворотом вокруг точкиOна углы соответственно 120° и 240°. Эти три семиугольника удовлетворяют условиям задачи.
Ответ

а), б) Существуют.

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет