Олимпиадная задача по стереометрии и теории чисел для 10–11 классов: раскраска рёбер n-угольной призмы
Задача
При каких n можно раскрасить в три цвета все ребра n-угольной призмы (основания – n-угольники) так, что в каждой вершине сходятся все три цвета и у каждой грани (включая основания) есть стороны всех трёх цветов?
Решение
Пусть призма покрашена требуемым образом; тогда в основании есть три ребра всех трёх цветов, идущие подряд (иначе основание раскрашено с периодом 2 в два цвета). Рассмотрим такую тройку и занумеруем цвета в ней против часовой стрелке. Несложно проверить, что раскраска этого участка однозначно определяет раскраску участка, находящегося над ним, соответствующих боковых рёбер и следующих рёбер основания (см. рис).
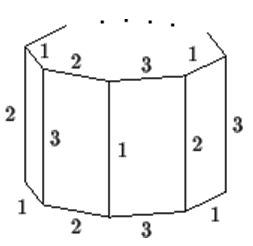
Ответ
Приn, кратных 3.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет