Олимпиадная задача по планиметрии о движении катера: максимальное расстояние до берега (Классы 8–10)

  а) Контрпример приведён на рисунке.

  Здесь  AC = 1000 м,  AB > 1400 м,  CD = 1 м.  Маршрут корабля должен пересекать отрезок AB, но расстояние от любой точки AB до одного из берегов больше 700 м.   б) Построим такой маршрут. Выберем часть плоскости по одну сторону от правого берега, содержащую левый берег, и рассмотрим множество точек, удалённых от правого берега не более чем на 800 м. Построить его можно так: возьмём красящий круг радиусом 800 м и протащим его центр вдоль правого берега. Тогда круг закрасит полосу, граница которой тянется вдоль реки (обозначим эту границу через L).

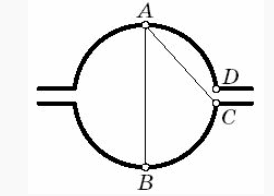
  Если L вся идёт по суше, то левый берег даст искомый маршрут. Если L – вся на воде, то рассмотрим L в качестве маршрута. Если L пересекает левый берег, то участки L вне реки заменим участками левого берега и рассмотрим полученный маршрут. Каждая точка такого маршрута отстоит от правого берега не больше чем на 800 м. Докажем, что и от левого берега тоже.

  Допустим, что это неверно, то есть найдётся точка на маршруте, удалённая от левого берега больше чем на 800 м. Тогда круг с центром в этой точке и радиусом 800 м целиком лежит на воде (кроме одной или нескольких точек правого берега на окружности). Докажем, что тогда найдётся точка на одном из берегов, расстояние от которой до другого берега больше 1000 м.

  Рассмотрим множество лучей с началом в центре O этого круга и покрасим их в два цвета: в синий, если первое пересечение луча происходит с правым берегом, и в красный – если с левым. Соответственно покрасим точки окружности. Покажем, что найдётся одноцветная дуга окружности величиной не меньше 180°. Для этого докажем, что окружность состоит не больше чем из двух разноцветных дуг.

  Допустим, что это неверно и разноцветных дуг больше двух. Поскольку дуги чередуются, то их чётное число. Возьмём по одной точке на четырёх соседних дугах: краснуюК'₁, синююС'₁, краснуюК'₂, синююС'₂, и соответствующие им точки первого пересечения лучей с берегами:К₁,С₁,К₂,С₂(рис. слева).   Береговая линия междуК₁иК₂должна пересекать один из лучейOС₁,OС₂(пустьОС₁), причём дальше от центра, чемС₁. Рассмотрим контур, состоящий из береговой линии междуК₁иК₂и отрезковOК₁иOК₂. Этот контур разделяет точкиС₁иС₂, поэтому береговая линия междуС₁иС₂должна его пересечь, но это невозможно (поскольку берега не пересекаются и есть правило раскраски). Следовательно, дуг ровно две, так как из точкиОвидны оба берега, а тогда найдётся одноцветная дуга (пусть красная) не меньше 180°.   Возьмём концы этой дугиК'₁,К'₂, её серединуК'₃и соответствующие точки берегаК₁,К₂,К₃(рис. справа).   Построим контур, состоящий из береговой линии междуК₁иК₂и отрезковOК₁иOК₂. Кратчайший путь отК₃до другого берега пересекает один из отрезковOК₁,OК₂. Следовательно, этот путь будет виден из точкиOпод углом не меньше 90°, но такой путь с концами вне круга будет не короче   800> 1000 м.  Это противоречит условию.   Итак, круг с центром на указанном маршруте радиусом 800 м поместить между берегами невозможно, поэтому всегда будет точка левого берега, отстоящая от указанного маршрута меньше чем на 800 м.

а) Не всегда;  б) всегда.