Олимпиадная задача Фомина: расстояние между центрами часов на стене (Планиметрия, 8–10 класс)
Задача
На стене висят двое правильно идущих совершенно одинаковых часов. Одни показывают московское время, другие – местное. Минимальное расстояние между концами их часовых стрелок равно m, а максимальное – M. Найдите расстояние между центрами этих часов.
Решение
В обозначениях риcунка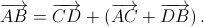 
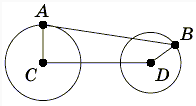
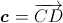постоянен, вектор 
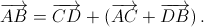имеет постоянную длину и равномерно вращается по окружности. Длина вектора c + a достигает максимума и минимума, когда векторы c и a коллинеарны. Поэтому длина вектора c равна полусумме минимального и максимального значений длины вектора c + a.
Ответ
½ (M + m).
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет