Олимпиадная задача по многочленам и последовательностям для 7–9 классов (Манукян С.)
Задача
Докажите, что при любом натуральном n 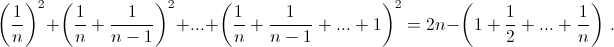
Решение
Дробь 1/k встречается в последних k скобках левой части, поэтому восле раскрытия скобок 1/k² встретится k раз (что даст в сумме 1/k), а дробь 2/kl для каждого
l > k – тоже k раз (что даст в сумме 2/l ). При этом каждому l отвечают l – 1 значений k. Следовательно, вся сумма равна 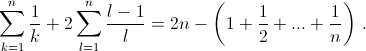
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет