Олимпиадная задача Фомина: о произведениях пятизначных и десятизначных числах

  Количество десятизначных чисел, представимых в виде произведения двух пятизначных, не больше количества всех пар пятизначных чисел (с учетом пар одинаковых чисел). (На самом деле их значительно меньше: во-первых, не все произведения, двух пятизначных чисел будут десятизначными, во-вторых, разные пары чисел могут дать одно и то же произведение.) Поэтому достаточно проверить, что количество пар пятизначных чисел меньше половины количества десятизначных чисел. Первый способ. Всего десятизначных чисел 9·10⁹(см. решение задачи160336), а удвоенное количество пар пятизначных чисел равно   9·10⁴(9·10⁴+ 1) = 81·10⁸+ 9·10⁴< 9·10⁹.  Второй способ. Каждой паре  (A,B)  двух различных пятизначных чисел можно поставить в соответствие два десятизначных числа 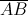   и 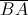   (записав их друг за другом). Каждой паре вида  (A,B)  также поставим в соответствиедвачисла:  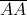  и 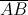    Заметим, что так получаются не все десятизначные числа: число 1111101111 так получить нельзя. Поэтому пар пятизначных чисел меньше половины количества десятизначных.

Больше непредставимых.