Назад

Олимпиадная задача по алгебраическим методам: сумма чисел на шахматной доске (7-9 класс)

Задача 197957 • Сложность: 3 • 7-9 класс
Задача

В клетки шахматной доски записаны числа от 1 до 64 (первая горизонталь нумеруется слева направо числами от 1 до 8, вторая от 9 до 16 и т. д.). Перед некоторыми числами поставлены плюсы, перед остальными – минусы, так что в каждой горизонтали и в каждой вертикали по четыре плюса и по четыре минуса. Докажите, что сумма всех чисел равна 0.

Авторы:
Фольклор
Разделы:
Текстовые задачи Алгебраические методы
Источники:
Турнир городов 9 турнир (1987/1988 год) весенний тур, тренировочный вариант, 7-8 класс Олимпиады и турниры
Количество версий:
5
Решение
Понятно, что если в каждой строке первой доски-слагаемого поставить по четыре минуса, то сумма всех её чисел будет равна нулю. Аналогично если расставить по четыре минуса в каждом столбце второй доски-слагаемого, то сумма всех её чисел будет равна нулю. Значит, при указанной в условии расстановке знаков сумма всех чисел на исходной доске будет равна нулю.
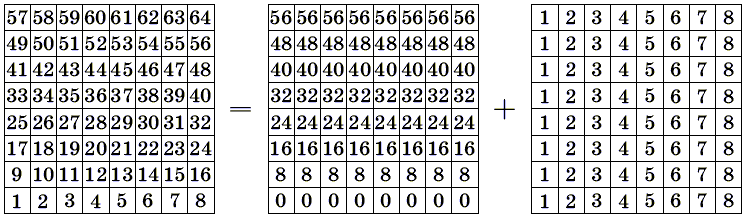
Ответ

Ответ задачи отсутствует

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет