Назад

Олимпиадная задача по планиметрии: треугольники, точка внутри и принцип крайнего

Задача 197946 • Сложность: 3 • 8-9 класс
Задача

Три треугольника – белый, зелёный и красный – имеют общую внутреннюю точку M. Докажите, что можно выбрать по одной вершине из каждого треугольника так, чтобы точка M находилась внутри или на границе треугольника, образуемого выбранными вершинами.

Решение

  Рассмотрим всевозможные углы, образуемые отрезками, идущими из M в некоторые две вершины разного цвета. Пусть наибольший из этих углов – ∠AMB ≤ 180°, причём A – красная точка, B – белая. Тогда внутри углов AMB' и BMA', смежных с углом AMB, нет зелёных вершин (см. рис.).

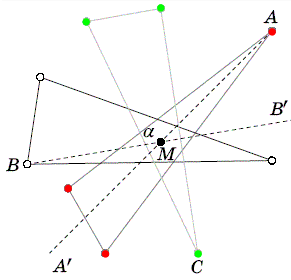
  Поэтому в вертикальном по отношению к углу AMB угле A'MB' должна найтись хотя бы одна зелёная вершина C (иначе все три зелёные вершины оказались бы внутри угла AMB, и зелёный треугольник не содержал бы внутри себя точку M). Треугольник ABC – искомый: он содержит точку M, поскольку M лежит по одну сторону с C от прямой AB, а отрезки AC и BC пересекают продолжения отрезков BM и AM соответственно.
Ответ

Ответ задачи отсутствует

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет