Олимпиадная задача по планиметрии и комбинаторной геометрии для 8-9 класса: вписанная окружность в четырёхугольники
Задача
Рассматривается выпуклый восьмиугольник. С помощью диагонали от него можно отрезать четырёхугольник, причём это можно сделать восемью способами. Может ли случиться, что среди этих восьми четырёхугольников имеется
а) четыре,
б) пять
таких, в которые можно вписать окружность?
Решение
а) Пример такого восьмиугольника: полуправильный восьмиугольник со сторонами 2 и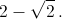 
От него можно четырьмя способами отрезать описанную трапецию со сторонами 
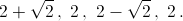б) Докажем, что это невозможно. Первый способ. Среди пяти диагоналей, отсекающих описанные четырёхугольники найдутся соседние, например, AD и BE. Тогда
AB + CD = BC + AD, BC + DE = CD + BE, значит, AB + DE = AD + BE. Это противоречит тому, что сумма длин диагоналей четырёхугольника больше суммы длин двух его противоположных сторон (см. зад. 155162). Второй способ. Пусть окружности с центрами P и Q вписаны в четырёхугольники ABCD и BCDE. Оба центра находятся на биссектрисе угла BCD. Кроме того, P лежит на биссектрисе угла ABC, а Q – на биссектрисе угла EBC. ∠EBC < ∠ABC, поэтому BQ < BP. Но аналогично (с использованием углов ADC и EDC вместо EBC и ABC) доказывается, что BP < BQ. Противоречие.
Ответ
а) Может; б) не может.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь