Задача
а) Из произвольной точки M внутри правильного n-угольника проведены перпендикуляры MK1, MK2, ..., MKn к его сторонам (или их продолжениям). Докажите, что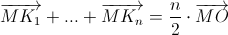 
(O – центр n-угольника). б) Докажите, что сумма векторов, проведённых из любой точки M
внутри правильного тетраэдра перпендикулярно к его граням, равна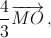 
где O – центр тетраэдра.
Решение
а) Пусть Li – середины сторон n-угольника.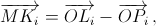 
где Pi – проекция точки M на прямую OLi. Как известно (см. задачи 155719,
155373 а),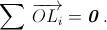 
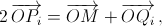где Qi – точка, симметричная M относительно прямой OLi. Заметим, что точки Qi получаются друг из друга поворотом на 4π/n вокруг точки O (например, Q2 получается из Q1 композицией двух симметрий относительно прямых OL1 и OL2, то есть поворотом на удвоенный угол между этими прямыми). Таким образом, Qi – вершины правильного многоугольника с центром O (число его сторон равно n, если n нечётно, и n/2, если n чётно; при n = 4 получается отрезок). Следовательно, 
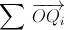также равна 0, а 
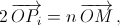что и доказывает утверждение. б) Пусть Li – центр грани, противоположной вершине Ai тетраэдра A1A2A3A4, Pi – проекция M на OLi. Как и в а),
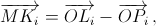
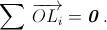
Заметим, что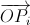 
линейно зависит от вектора 
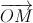(это просто проекция). Следовательно, и 
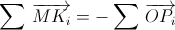линейно зависит от 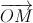. Но при M = A1 три слагаемых обращаются в нуль, и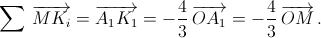 
Аналогичное равенство выполняется для каждой вершины тетраэдра, значит, оно верно и для любой точки M (поскольку вектор 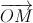есть линейная комбинация векторов 
).
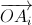Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь