Задача
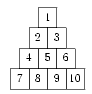
Переложите пирамиду из 10 кубиков (см. рисунок) так, чтобы её форма осталась прежней, но каждый кубик соприкасался только с новыми кубиками.
Решение
Заметим следующее: кубик, стоящий в центре, соприкасается с шестью кубиками; кубики, стоящие в вершинах, — с двумя; а кубики, стоящие на сторонах треугольника, — с четырьмя. Отсюда сразу можно заключить, что при новой перекладке кубик из центра может попасть только в вершину, а в центр, наоборот, — только из вершины.
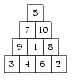
Для определённости, пусть в центр попадёт кубик 1, а кубик 5 — в верхнюю вершину. Тогда на место кубиков 2 и 3 могут лечь только кубики 7 и 10, поскольку остальные кубики уже соприкасались с кубиком 5 (рис. 1). В нижние вершины должны лечь кубики 2 и 3. Расположение остальных кубиков определим перебором. Окончательный вариант показан на рис. 2.

Ответ
См. рисунок справа.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь