Задача
Дан куб ABCDA1B1C1D1с ребром a . Пусть M – такая точка на ребре A1D1, для которой A1M:MD1 = 1:2. Найдите периметр треугольника AB1M , а также расстояние от вершины A1до плоскости, проходящей через вершины этого треугольника.
Решение
Из прямоугольных треугольников AA1M , B1A1M и AA1B1по теореме Пифагора находим, что
AM = 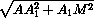 =
= 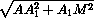 =
=
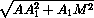 ,
,
B1M =  =
= 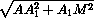 =
=
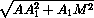 ,
,
AB1 = 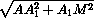 =
= 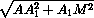 = a
= a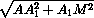 .
.
AM + B1M + AB1 = 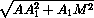 +
+ 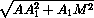 + a
+ a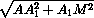 =
=
= 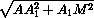 + a
+ a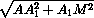 =
= 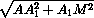
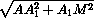 Пусть K – середина основания AB1равнобедренного треугольника MAB1. Тогда MK – высота треугольника MAB1. По теореме Пифагора
из прямоугольного треугольника MAK находим, что
Пусть K – середина основания AB1равнобедренного треугольника MAB1. Тогда MK – высота треугольника MAB1. По теореме Пифагора
из прямоугольного треугольника MAK находим, что
MK = 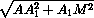 =
= 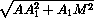 =
= 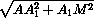 .
.
V = 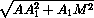 SΔ A1MB1· AA1 =
SΔ A1MB1· AA1 =
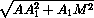 ·
· 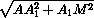 A1M· A1B1· AA1 =
A1M· A1B1· AA1 =
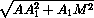 ·
· 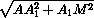 ·
· 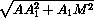 · a· a =
· a· a =  .
.
V = 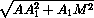 SΔ AB1M· h,
SΔ AB1M· h,
h = 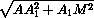 =
= 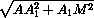 =
=
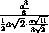 =
=
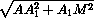 .
.
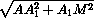 Примем за начало координат вершину A1, а оси
координат направим по лучам A1D1, A1B1и A1A . Тогда уравнение
плоскости, проходящей через точки A , B1и M , имеет вид
Примем за начало координат вершину A1, а оси
координат направим по лучам A1D1, A1B1и A1A . Тогда уравнение
плоскости, проходящей через точки A , B1и M , имеет вид
 +
+ 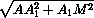 +
+ 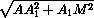 = 1
= 1
h = 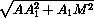 =
= 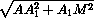 .
.
Ответ
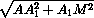 ;
; 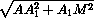 .
.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет