Задача
На плоскости α , проходящей через центр шара радиуса R , задана окружность с центром O1и радиусом r1, расположенная внутри шара. Все точки этой окружности соединены прямыми с точкой A , принадлежащей шару и удалённой от плоскости α на расстояние R . Множество отличных от A точек пересечения этих прямых с поверхностью шара является окружностью с центром O2и радиусом r2. Найдите расстояние от точки O2до плоскости α , если расстояние между точками A и O1равно a .
Решение
Пусть O – центр сферы. Выберем точку B на прямой OO2(перпендикулярной плоскости β ) так, чтобы для некоторой (а значит, для любой) точки K второй окружности прямая BK касалась сферы в точке K (рис.1). Тогда из прямоугольного треугольника BKO с высотой KO2, опущенной на гипотенузу, находим, что
OO2 = 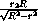 =
= 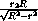 ,
BO =
,
BO =  =
= 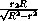 ,
,
BK = 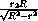 =
= 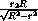 =
=
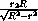 .
.
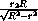 LC , т.к.
плоскость AON содержит прямые OA и ON , перпендикулярные LC ( ON
LC , т.к.
плоскость AON содержит прямые OA и ON , перпендикулярные LC ( ON 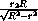 LC , т.к. прямая ON перпендикулярна плоскости ABK ). Значит, AN
LC , т.к. прямая ON перпендикулярна плоскости ABK ). Значит, AN 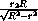 MB .
MB .
Так как BK – касательная к сфере, то BK 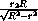 NK . Треугольник ANK –
равнобедренный, поэтому
NK . Треугольник ANK –
равнобедренный, поэтому
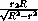 KMB = 90o -
KMB = 90o - 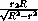 KAN = 90o -
KAN = 90o - 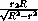 AKN =
AKN = 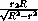 BKM, BM = BK.
BKM, BM = BK.
LC = BM·  = BK·
= BK·  =
=
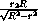 ·
·  =
=
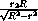 ,
,
 не зависит от выбора точки K на
второй окружности. Таким образом, точка C равноудалена от всех
точек первой окружности, а значит, является её центром, т.е.
совпадает с точкой O1.
не зависит от выбора точки K на
второй окружности. Таким образом, точка C равноудалена от всех
точек первой окружности, а значит, является её центром, т.е.
совпадает с точкой O1.
Рассмотрим сечение сферы плоскостью AOO2, содержащей перпендикуляр AO , а значит, и перпендикуляр O2D к плоскости α . Треугольники ALO1и AMB подобны с коэффициентом
k = 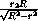 =
= 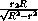 =
=
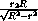 =
= 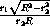 .
.
AB = 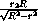 =
= 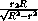 .
.
cos 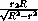 AOB =
AOB = 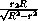 =
=
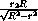 =
=
= 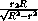 .
.
O2D = OO2 sin 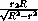 O2O1D = -
O2O1D = - 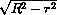 cos
cos 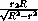 AOB =
AOB =
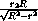 .
.
Ответ
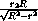 .
.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь