Задача
В кубе ABCDA1B1C1D1, где AA1, BB1, CC1и DD1– параллельные рёбра, плоскость P проходит через точку D и середины рёбер A1D1и C1D1. Найдите расстояние от середины ребра AA1до плоскости P , если ребро куба равно 2.
Решение
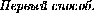 Пусть M , N , K и L – середины рёбер A1D1, C1D1, AA1и CC1соответственно (рис.1). Прямая KL параллельна прямой MN , поэтому прямая KL параллельна плоскости P . Кроме того, прямая KL проходит через центр O куба ABCDA1B1C1D1. Значит, расстояние от середины K ребра AA1до плоскости P равно расстоянию от точки O до этой плоскости.
Пусть M , N , K и L – середины рёбер A1D1, C1D1, AA1и CC1соответственно (рис.1). Прямая KL параллельна прямой MN , поэтому прямая KL параллельна плоскости P . Кроме того, прямая KL проходит через центр O куба ABCDA1B1C1D1. Значит, расстояние от середины K ребра AA1до плоскости P равно расстоянию от точки O до этой плоскости.
Пусть E – точка пересечения отрезков MN и B1D1, F – основание
перпендикуляра, опущенного из точки O на прямую DE . Так как прямая MN перпендикулярна плоскости BB1D1D , то MN  OF . Значит, OF –
перпендикуляр к плоскости P . Таким образом, искомое расстояние
равно длине отрезка OF .
OF . Значит, OF –
перпендикуляр к плоскости P . Таким образом, искомое расстояние
равно длине отрезка OF .
Рассмотрим сечение данного куба плоскостью BB1D1D (рис.2). Пусть прямая, проходящая через середину O диагонали BD1параллельно BD , пересекает отрезок DE в точке Q , а отрезок DD1– в точке S . Тогда OS – средняя линия треугольника BD1D , а QS – средняя линия треугольника EDD1. Поэтому
OQ = OS - QS = 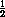 BD -
BD - 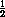 ED1 =
ED1 = 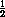 (BD - ED1) =
(BD - ED1) =
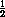 (2
(2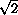 -
- 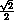 ) =
) = 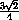 .
.
 FOQ = α . Тогда
FOQ = α . Тогда
 EDD1 =
EDD1 =  FOQ = α,
cos α =
FOQ = α,
cos α = 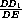 =
= 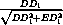 =
=
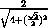 =
= 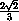 .
.
OF = OQ cos α = 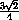 ·
· 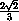 = 1.
= 1.
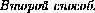 Выберем прямоугольную систему координат D1xyz , взяв за начало
точку D1и направив оси координат по лучам D1A1, D1C1и D1D соответственно. Уравнение плоскости P будет иметь вид
Выберем прямоугольную систему координат D1xyz , взяв за начало
точку D1и направив оси координат по лучам D1A1, D1C1и D1D соответственно. Уравнение плоскости P будет иметь вид
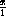 +
+ 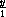 +
+ 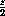 = 1
= 1
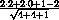 =
=  = 1.
= 1.
Ответ
1.00
Чтобы оставлять комментарии, войдите или зарегистрируйтесь