Задача
На плоскости лежат три равных конуса с общей вершиной. Каждый из них касается двух рядом лежащих. Найдите угол при вершине каждого конуса.
Решение
Пусть ABCD – правильная треугольная пирамида с вершиной D , O – центр её основания ABC . Рассмотрим три конуса с общей вершиной O , вписанных в треугольные пирамиды OABD , OBCD и OACD ("каркасы" конусов) так, что их основания вписаны в треугольники ABD , BCD и ACD соответственно, причём каждые два конуса имеют ровно одну общую образующую.
Пусть O1– центр основания конуса, вписанного в пирамиду OABD ,
а OK – образующая этого конуса, являющаяся также образующей конуса,
вписанного в пирамиду OBCD . Тогда O1K 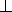 BD , поэтому по теореме о
трёх перпендикулярах OK
BD , поэтому по теореме о
трёх перпендикулярах OK 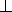 BD , значит, OK – высота прямоугольного
треугольника OBD , проведённая из вершины прямого угла.
BD , значит, OK – высота прямоугольного
треугольника OBD , проведённая из вершины прямого угла.
Обозначим AB = BC = AC = a . Если M – середина AB , то
OK = OM = 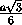 , OB =
, OB = 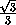 ,
cos
,
cos  BOK =
BOK = 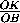 =
= 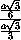 =
= 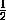 ,
,
 BDO =
BDO =  BOK = 60o . Следовательно,
BOK = 60o . Следовательно,
DO = OB ctg 60o = 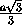 ·
· 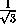 =
= 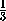 a.
a.
tg α = tg  MOO1= tg
MOO1= tg  MDO =
MDO = 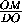 =
= 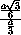 =
= 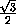 ,
,
cos 2α = 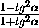 =
= 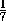 .
.
Ответ
2 arctg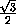 = 2 arccos
= 2 arccos 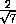 =
arccos
=
arccos 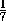 .
.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь