Решение 1:  Поместим в каждую вершину массу, обратную длине проведённой из этой вершины касательной к сферы (все три касательные для данной вершины, очевидно, равны). Тогда точка касания ребра совпадает с центром масс его концов, и, следовательно, все три отрезка из условия пересекаются в центре масс полученной системы материальных точек.

Решение 2:  ПустьK, L, M, N, P, R– точки, в которых соответственно рёбраAB, AC, AD, BC, BD, CDтетраэдраABCDкасаются сферы,a, b, c, d– длины касательных, выходящих соответственно из вершинA, B, C, D.   ПлоскостиABDиBCDпересекаются по прямойBD. По теореме Менелая (применённой к треугольникуABD) прямаяMKпересекаетBDв точке, делящей отрезокBD(внешним образом) в отношении 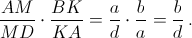   По той же причине прямаяRNпересекаетBDв той же точке, так как  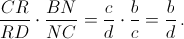  (Если  b = d,  тоMKиRNпараллельныBD.) Значит, прямыеMKиRNлежат в одной плоскости (пересекаются или параллельны). Следовательно, прямыеMNиKRтакже пересекаются (почему они не параллельны?!).   Аналогично, прямаяLPпересекаетMNиKR. Поскольку эти три прямые очевидно не лежат в одной плоскости, они должны пересекаться в одной точке.

Ответ задачи отсутствует