Задача
С выпуклым четырехугольникомABCDпроделывают следующую операцию: одну из данных вершин меняют на точку, симметричную этой вершине относительно серединного перпендикуляра к диагонали (концом которой она не является), обозначив новую точку прежней буквой. Эту операцию последовательно применяют к вершинамA,B,C,D,A,B,... - всегоnраз. Назовем четырехугольник допустимым, если его стороны попарно различны и после применения любого числа операций он остается выпуклым. Существует ли: а) допустимый четырехугольник, который послеn<5 операций становится равным исходному; б) такое числоn0, что любой допустимый четырехугольник послеn=n0операций становится равным исходному?
Решение
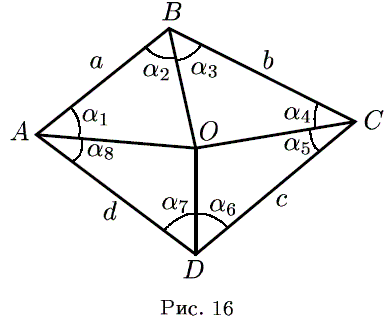
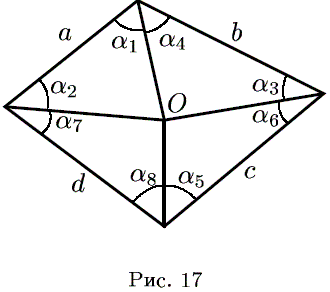
Обозначим черезOточку пересечения серединных перпендикуляров к диагоналям. Заметим, что эта точка остаётся на месте при применении любого количества операций к четырёхугольнику. Обозначим через α1, α2, …, α8углы, образованные сторонами четырёхугольника и отрезкамиAO,BO,CO,DO(см. рис. 16). После применения трёх операций стороны четырёхугольника опять будут стоять в прежнем порядке:a,b,c,d, а указанные углы будут расположены, как указано на рис. 17.
Если α1+ α4= α2+ α3и α6+ α7= α5+ α8, то четырёхугольникABCDвписанный. При этом он перейдёт в равный ему четырёхугольник за три операции.
После шести операций стороны опять будут расположены в прежнем порядке и углы будут расположены так, как показано на рис. 16.
Ответ
а) ЕслиABCD- вписанный четырёхугольник, то он перейдёт в равный четырёхугольник за три операции. б) Любой допустимый четырёхугольник перейдёт в равный ему четырёхугольник за 6kопераций, гдеk- произвольное натуральное число (например, заn0= 6 операций).
Чтобы оставлять комментарии, войдите или зарегистрируйтесь