Обозначим серединуAPчерезA₁, серединуBCчерезA₂, проекцию точкиPнаBCчерезA₃. ТочкиB₁,B₂,B₃иC₁,C₂,C₃определим аналогично. Обозначим точку пересечения описанных окружностей треугольниковB₁C₂A₁иC₁B₂A₁черезQ. Докажем, что описанная окружность треугольникаC₁B₁A₂тоже содержит точкуQ. Заметим, чтоA₁QC₁= 180° −A₁B₂C₁= 180° −A₁PC₁. АналогичноA₁QB₁= 180° −A₁PB₁. Значит, B₁QC₁=A₁QB₁+A₁QC₁= 360° −A₁PC₁−A₁PB₁=B₁PC₁=B₁A₂C₁. Следовательно, описанная окружность треугольникаC₁B₁A₂тоже содержит точкуQ. Аналогично доказывается, что описанная окружность треугольникаA₂B₂C₂тоже содержит точкуQ. Осталось доказать, что описанная окружность треугольникаA₃B₃C₃тоже содержит точкуQ. Для этого достаточно показать, чтоA₃C₃B₃=A₃QB₃. ТочкаC₃симметрична точкеPотносительноA₁B₁. Значит,A₁C₃B₁=A₁PB₁=A₁C₂B₁. Поэтому точкаC₃лежит на описанной окружности треугольникаA₁C₂B₁. 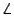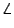Так как точкиA₁,B₃,B₂,C₁,Qлежат на одной окружности и четырёхугольникAB₃PC₃вписанный (поскольку углыB₃иC₃в нём прямые), тоB₃QC₁=B₃A₁C₁=C₁A₁P=PAB₃=B₃C₃P. АналогичноA₃C₃P=A₃QC₁. Значит, A₃C₃B₃=A₃C₃P+B₃C₃P=B₃QC₁+A₃QC₁=A₃QB₃, что и требовалось доказать. Другие случаи расположения точек рассматриваются аналогично.

Ответ задачи отсутствует