Назад
Задача 186102 • Сложность: 2 • 8-10 класс
Задача

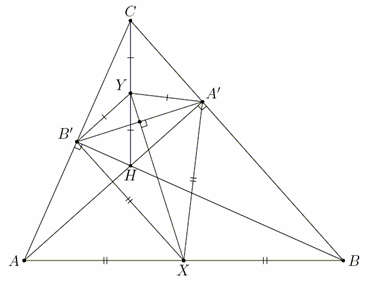
Высоты AA' и BB' треугольника ABC пересекаются в точке H. Точки X и Y – середины отрезков AB и CH соответственно.

Доказать, что прямые XY и A'B' перпендикулярны.

Решение

  Докажем, что точки X и Y лежат на серединном перпендикуляре к отрезку A'B'. Для этого достаточно проверить, что X и Y равноудалены от A' и B'.   Первый способ. В треугольниках CA'H и CB'H медианы прямых углов равны половине гипотенузы, поэтому  A'Y = ½ CH = B'Y.  Аналогично

A'X = B'X.

  Второй способ. Отрезки AB и CH видны из точек A' и B' под прямыми углами, поэтому A' и B' лежат на окружности с диаметром AB и на окружности с диаметром CH. Значит, A' и B' равноудалены от центров X и Y этих окружностей.
Ответ

Ответ задачи отсутствует

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет