Рассмотрим число  A = 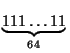0.  Оно делится на  1111 = 11·101,  поэтому A делится на 101. Сопоставим каждому 64-значному числу  n = a₁a₂...a₆₄,  не содержащему в записи нулей и делящемуся на 101, число  A – n = (10 – a₁)(10 – a₂)...(10 – a₆₄).  Это число тоже не содержит в записи нулей и делится на 101. Равенство  n = A – n  возможно лишь в том случае, когда &n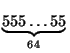bspn = .  Остальные рассматриваемые числа разбиваются на пары. Поэтому общее количество всех таких чисел нечётно.

Не является.