Ответ:n= 50. Заметим сначала, что 50 треугольников достаточно. В самом деле, пусть$\Delta_{k}^{}$— треугольник, стороны которого лежат на лучахA_kA_{k - 1}иA_kA_{k + 1}и который содержит выпуклый многоугольникA₁...A₁₀₀. Тогда этот многоугольник является пересечением треугольников$\Delta_{2}^{}$,$\Delta_{4}^{}$, ...,$\Delta_{100}^{}$. С другой стороны, 100-угольник, изображённый на рисунке, нельзя представить в виде пересечения менее чем 50 треугольников.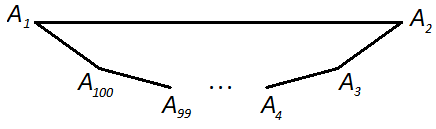В самом деле, если три его стороны лежат на сторонах одного треугольника, то одна из этих сторон -- сторонаA₁A₂. Все стороны этого многоугольника лежат на сторонахnтреугольников, поэтому2n+ 1$\ge$100, т.е.n$\ge$50.

Ответ задачи отсутствует