Задача
Существуют ли рациональные числаa,b,c,d, удовлетворяющие равенству
(a + b$\displaystyle \sqrt{2}$)2n + (c + d$\displaystyle \sqrt{2}$)2n = 5 + 4$\displaystyle \sqrt{2}$
(гдеn— натуральное число)?
Решение
Ответ:нет, не существуют.
Прежде всего заметим, что представление числа в видеp+q$\sqrt{2}$, гдеpиq— рациональные числа, единственно, т.е. еслиp + q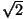 
= p1 + q1$\sqrt{2}$, где все числаp,q,p1,q1рациональные, тоp=p1иq=q1. Действительно,q=q1, поскольку иначе$\sqrt{2}$=${\frac{p-p_1}{q_1-q}}$— рациональное число. Поэтомуp=p1.
Пустьp,q,r,s— рациональные числа. Тогда
(p + q$\displaystyle \sqrt{2}$)(r + s$\displaystyle \sqrt{2}$) = pr + 2qs + (ps + qr)$\displaystyle \sqrt{2}$,
Поэтому если существуют рациональные числаa,b,c,d, удовлетворяющие указанному равенству, то
(p - q$\displaystyle \sqrt{2}$)(r - s$\displaystyle \sqrt{2}$) = pr + 2qs - (ps + qr)$\displaystyle \sqrt{2}$.
(a - b$\displaystyle \sqrt{2}$)2n + (c - d$\displaystyle \sqrt{2}$)2n = 5 - 4$\displaystyle \sqrt{2}$ < 0.
Этого не может быть, поскольку числа (a-b$\sqrt{2}$)2nи
(c-d$\sqrt{2}$)2nнеотрицательны.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет