Задача
Известно, что an – bn делится на n (a, b, n – натуральные числа, a ≠ b). Доказать, что 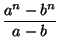 делится на n.
делится на n.
Решение
Воспользуемся методом математической индукции.
База. Пусть n – простое число. Если число a – b не делится на n, то всё ясно. Если же a ≡ b (mod n), то
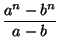 = an–1 + an–2b + ... + abn–2 + bn–1 ≡ nbn–1 ≡ 0 (mod n).
= an–1 + an–2b + ... + abn–2 + bn–1 ≡ nbn–1 ≡ 0 (mod n).
Шаг индукции. Пусть для всех показателей, меньших n, утверждение доказано. Обозначим d = НОД(n, a – b), тогда n = kd.
Если d = 1, то все ясно. Если d = n, то a ≡ b (mod n), и можно повторить вышеприведённое доказательство.
Если же 1 < d < n, то 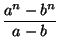 делится на n, так как первый множитель делится на k, а второй – на d (у последней дроби знаменатель, а тем более числитель делится на d).
делится на n, так как первый множитель делится на k, а второй – на d (у последней дроби знаменатель, а тем более числитель делится на d).
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь