Докажем индукцией по n , что число различных дуг после n засечек не превосходит3. Для n=2это очевидно. Обозначим через A_k засечку с номером k . Пусть сделано n засечек и точка A_n попала на ДУГУ A_kA_l . Тогда точка A_n-1попадает на дугу A_k-1A_l-1. Поэтому при k,l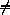 1новых длин не появится, и требуемое утверждение доказано. Предположим теперь, что, например, l=1. Докажем, что тогда длина любой дуги A_pA_q между соседними засечками равна длине одной из дуг A_kA₁ , A_nA₁ , A₁A_s , где A_s – ближайшая к A₁ засечка, отличная A_n . Действительно, при p,q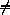 1длина дуги A_pA_q равна длине дуги A_p-1A_q-1, а между засечками A_p-1и A_q-1нет других засечек, кроме возможно, A_n . Таким образом за конечное число шагов мы приходим к одной из рассматриваемых трех дуг.

не более трех.