Ответ:x=4,y=6. Пусть A=89252525...2525, B=444x18y27. Представим число B в виде суммы B=444x00y00+18027. Произведение A· 18027имеет вид3..272727272727268175, в частности, его53-я цифра равна7, а54-я равна2. Пусть число C· (B-18027)/4записывается цифрами111abcdef . Тогда AB=A· 18027+4A· (B-18027)/4= 3..2727272727268175+3..1010101010100· C . Будем производить умножение и сложение 'в столбик'. Тогда53-я цифра в числе AB будет равна7+1+1+b+d+f+x , где x – число десятков, которые мы переносим из52-го разряда. Цифра с номером54равна2+1+a+c+e+y , где y – число десятков, которые мы переносим из53-го разряда. Ясно, что x 4. Заметим, что a,d0;1;2, b,e 0;2;5;7, c,f0;5, причем b и c не могут быть равны5одновременно. Из этого получаем оценку7+1+1+b+d+f+x 7+1+1+7+2+5+4=27, откуда y 2. Но по условию53-я цифра суммы равна1, поэтому y 1. Далее,2+1+a+c+e+y 2+1+2+5+7+2=19. Но последняя цифра этого числа равна нулю, поэтому2+1+a+c+e+y=10. В частности, из54-го разряда в55-й мы переносим ровно1десятков. Но из вида наших слагаемых следует, что из54-го разряда в55-й мы переносим столько же десятков, сколько из52-го в53-й. Следовательно, x=1. Получаем, что должна выполняться совокупность двух систем уравнений: либо2+1+a+c+e+2=10,7+1+1+b+d+f+1=21(1), либо2+1+a+c+e+1=10,7+1+1+b+d+f+1=11(2). Поскольку каждая из цифр a,b,c,d,e,f может принимать небольшое число значений, несложным перебором находим единственное решение abcdef=100150(учитываем, что цифры bc,ef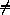 05,55).

x=4,y=6.