Задача
Улитка должна проползти вдоль линий клетчатой бумаги путь длины 2n, начав и кончив свой путь в данном узле.
Доказать, что число различных её маршрутов равно 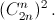
Решение
При любом таком маршруте число ходов вверх равно числу ходов вниз, а число
ходов вправо равно числу ходов влево. Выпишем на один лист бумаги номера ходов, ведущих вправо или вверх, а на другой — номера ходов, ведущих влево или вверх. На каждом листе будет выписано ровно n номеров.
По каждой паре таких наборов маршрут однозначно восстанавливается (например, если номер входит в оба набора, то ему соответствует ход вверх). Этот маршрут замкнутый, поскольку число ходов вправо равно числу ходов влево (оба они дополняют число ходов вверх до n), а число ходов вверх равно числу ходов вниз (вычитая из общего числа 2n ходов число ходов вправо, влево и вверх, мы, с одной стороны, получим число ходов вниз, а с другой стороны, – число ходов вверх). Итак, число маршрутов равно числу пар наборов из n номеров,
то есть 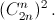
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь