Задача
a, bиn– натуральные числа, иnнечётно. Докажите, что если числитель и знаменатель дроби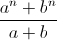 
делятся наn, то и сама дробь делится наn.
Решение
По условию a ≡ – b (mod n), а значит, 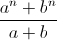= an–1 – an–2b + ... – abn–1 + bn ≡ nbn–1 ≡ 0 (mod n).
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет