Задача
В школе изучают 2n предметов. Все ученики учатся на 4 и 5. Никакие два
ученика не учатся одинаково, ни про каких двух нельзя сказать, что один из них
учится лучше другого. Доказать, что число учеников в школе не больше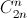 
.
(Мы считаем, что ученик p учится лучше ученика q, если у p оценки по всем предметам не ниже, чем у q, а по некоторым предметам – выше.)
Решение
Немного изменим условие: пусть в школе учатся 22n учеников со всевозможными наборами пятёрок и четвёрок. Выберем из них максимальную группу A попарно несравнимых учеников (в смысле условия задачи). Мы докажем, что эта группа состоит в точности из всех учеников, которые имеют ровно n пятёрок (их ровно 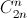). Отсюда, очевидно, следует утверждение исходной задачи.
Выделим в A подгруппу B, состоящую из учеников с наименьшим числом k пятёрок. Пусть k < n. Рассмотрим группу C всех учеников, каждый из которых имеет пятёрки ровно по k + 1 предмету, причём он (учится) лучше одного из учеников группы B. Очевидно ни один из них не входит в A, и мы можем заменить группу B на группу C. Докажем, что число c учеников группы C больше, чем число b учеников группы B.
Пусть каждый ученик группы B пожмёт руку всем ученикам из C, которые лучше него (таких учеников ровно 2n – k). Всего будет сделано
(2n – k)b > (k + 1)b рукопожатий. Действительно, 2k + 1 ≤ 2(n – 1) + 1 < 2n. С другой стороны, каждый ученик из C пожал руки не более, чем k + 1 ученику, следовательно, (k + 1)c > (k + 1)b, то есть c > b.
Итак, заменив группу B на группу C, мы увеличим группу A, что противоречит ее максимальности. Противоречие доказывает, что k ≥ n.
Симметричным образом, доказывается, что в A нет учеников с числом пятёрок, большим n. Следовательно, A состоит только из учеников с n пятёрками, и (снова в силу максимальности) туда должны попасть все такие ученики.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь