Пусть , и – построенные векторы единичной длины.   Первый способ. Построим также вектор     Точка O лежит внутри треугольника ABC, поэтому луч OC₂ лежит внутри угла A₁OB₁. Достроим треугольник A₁OB₁ до ромба A₁OB₁D. Тогда     и 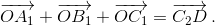    Пусть S – окружность радиуса 1 с центром D. Точка C₂ лежит на образе дуги A₁B₁ этой окружности при симметрии относительно прямой A₁B₁. Следовательно, точка C₂ лежит внутри окружности S, то есть  C₂D ≤ 1,  что и требовалось.   Второй способ  Точка O лежит внутри треугольника ABC, поэтому треугольник A₁B₁C₁ остроугольный. Пусть H – ортоцентр треугольника A₁B₁C₁. Он лежит внутри описанной окружности треугольника A₁B₁C₁, поэтому  OH ≤ 1.  Но согласно задаче 157693   .

Ответ задачи отсутствует