Пусть сумма первых двух цифр равнаn, и сумма двух последних цифр тоже равнаn. Числоnпринимает значение от 1 до 18. Если количество двузначных номеров, у которых сумма цифр равнаn, равноa_n, то искомое число равно 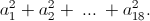     Двузначный номер, у которого сумма цифр равнаn, состоит из цифрaи  n–a,   где   0 ≤a≤ 9   и   0 ≤n–a≤ 9.   Таким образом,   0 ≤a≤ 9   и   n– 9 ≤a≤n.   Если  n≤ 9, то имеется  n+ 1  вариант:aпринимает значения от 0 доn. Если   9 <n≤ 18,   имеем  19 –n  вариантов:aпринимает значения от  n– 9  до 9. В итоге получаем   a₁= 2, a₂= 3,  ..., a₈= 9,  a₉= 10, a₁₀= 9,  ..., a₁₇= 2, a₁₈= 1.

669 номеров.