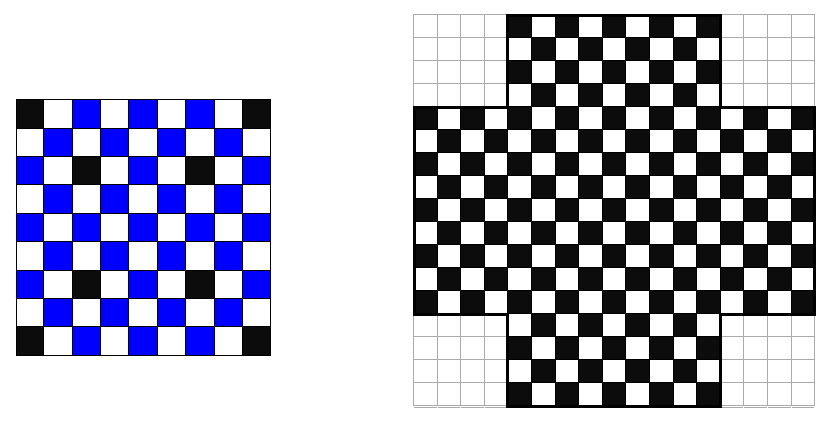
Пусть для определённости конь стоит на чёрной клетке. Все клетки, куда он может попасть за два хода, окрашены в синий цвет на рисунке слева. Случай

n = 1  исключительный.

  При  n> 1  множество клеток, куда может попасть конь за 2nходов, устроено следующим образом. Возьмём квадрат со стороной  8n+ 1  (конь стоит в центре этого квадрата). Отрежем от этого квадрата четыре уголка со стороной 2n(на рисунке справа соответствующая фигура изображена для  n= 2).  За 2nходов конь может попасть в точности во все чёрные клетки полученной фигуры. Докажем это.   Прежде всего заметим, что после нечётного числа ходов конь попадает на белую клетку, а после чётного – на чёрную. Индукцией поmнесложно доказать, что если  m≥ 3,  то заmходов конь попадает в любую клетку соответствующего цвета (чёрного при чётномmи белого при нечётномm) фигуры, которая получается при отрезании от квадрата со стороной  4m+ 1  четырёх уголков со сторонойm. При  m= 3  это легко проверяется, а шаг индукции очевиден.

Ответ задачи отсутствует