Такая окружность S может пересекать сторону клетки только в вершине. Поэтому каждую чёрную клетку, которую она "задевает", она пересекает по дуге, соединяющей две вершины.   Пусть окружность S проходит через две вершины A и B чёрной клетки. Рассмотрим два случая.

  1) Вершины A и B соседние. Рассмотрим другую чёрную клетку вершиной A. Окружность S проходит либо через соседнюю (ту, которая не лежит на прямой AB), либо через противоположную вершину этой клетки. В первом случае радиус окружности S равен 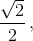    а во втором –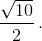  

  2) Вершины A и B противоположные. Снова рассмотрим другую чёрную клетку вершиной A. Теперь окружность S обязательно проходит через соседнюю с A вершину другой клетки. Радиус такой окружности равен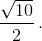  

  В итоге получаем, что наибольший радиус имеет следующая окружность S. Возьмём чёрную клетку и рассмотрим прилегающие к ней белые клетки. Окружность S проходит через восемь вершин этих белых клеток, отличных от вершин исходной чёрной клетки.

Ответ задачи отсутствует