Задачи и олимпиады по математике

Задача

Некоторые из чиселa₁,a₂,...a_nравны +1, остальные равны -1. Доказать, что

2 sin$\displaystyle \left(\vphantom{ a_1+\frac{a_1a_2}{2}+\frac{a_1a_2a_3}{4}+\dots +\frac{a_1a_2\cdot\ldots\cdot a_n}{2^{n-1}}}\right.$a₁ + $\displaystyle {\frac{a_1a_2}{2}}$ + $\displaystyle {\frac{a_1a_2a_3}{4}}$ + ... + $\displaystyle {\frac{a_1a_2\cdot\ldots\cdot a_n}{2^{n-1}}}$$\displaystyle \left.\vphantom{ a_1+\frac{a_1a_2}{2}+\frac{a_1a_2a_3}{4}+\dots +\frac{a_1a_2\cdot\ldots\cdot a_n}{2^{n-1}}}\right)$$\displaystyle {\frac{\pi}{4}}$ =

= a₁$\displaystyle \sqrt{2+a_2\sqrt{2+a_3\sqrt{2+\dots +a_n\sqrt{2}}}}$.

В частности, приa₁=a₂= ... =a_n= 1, имеем:

2 sin$\displaystyle \left(\vphantom{ 1+\frac{1}{2}+\frac{1}{4}+\dots +\frac{1}{2^{n-1}}}\right.$1 + $\displaystyle {\textstyle\frac{1}{2}}$ + $\displaystyle {\textstyle\frac{1}{4}}$ + ... + $\displaystyle {\frac{1}{2^{n-1}}}$$\displaystyle \left.\vphantom{ 1+\frac{1}{2}+\frac{1}{4}+\dots +\frac{1}{2^{n-1}}}\right)$$\displaystyle {\frac{\pi}{4}}$ = 2 cos$\displaystyle {\frac{\pi}{2^{n+1}}}$ =

= $\displaystyle \sqrt{2+\sqrt{2+\dots +\sqrt{2}}}$.

Решение

Применим индукцию поn. Приn= 1 получаем очевидное тождество. Равенство $\begin{align*} &2\left ( a_1+\frac{a_1a_2}{2}+\frac{a_1a_2a_3}{4}+\dots +\frac... ...frac{a_2a_3\cdot\ldots\cdot a_{n+1}}{2^{n-1}}\right )\frac{\pi}{4} \end{align*}$ показывает, что $\begin{align*} &\cos 2\left ( a_1+\frac{a_1a_2}{2}+\frac{a_1a_2a_3}{4}+\dots +... ...rac{a_2a_3\cdot\ldots\cdot a_{n+1}}{2^{n-1}}\right )\frac{\pi}{4}. 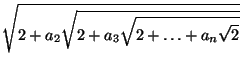\end{align*}$ Воспользовавшись этой формулой и тождеством2 sin${\frac{\alpha}{2}}$= ±$\sqrt{2-2\cos\alpha}$, получим $\begin{align*} &2\sin\left ( a_1+\frac{a_1a_2}{2}+\frac{a_1a_2a_3}{4}+\dots +\... ...a_2a_3\cdot\ldots\cdot a_na_{n+1}}{2^{n-1}}\right )\frac{\pi}{4}}. \end{align*}$ Нетрудно также убедиться, что в действительности всегда берётся знак плюс, поскольку знак числаa₁+${\frac{a_1a_2}{2}}$+${\frac{a_1a_2a_3}{4}}$+ ... +${\frac{a_1a_2\cdot\ldots\cdot a_na_{n+1}}{2^{n}}}$совпадает со знаком числаa₁. Теперь, воспользовавшись предположением индукции, получаем требуемое тождество.

Ответ

Ответ задачи отсутствует

Задача

Решение

Ответ

Подтверждение удаления