Решение 1:Обозначим через x среднее арифметическое данных чисел. Тогда они равны  x – ³/₂,  x – ¹/₂,  x + ¹/₂,  x + ³/₂,  а их произведение, увеличенное на 1, равно 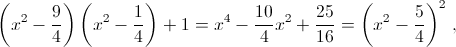     то есть является квадратом рационального числа. Поскольку это число целое, оно является квадратом целого числа.

Решение 2:Заметим, что  (a² – 1)(b² – 1) = (ab – 1)² – (a – b)²  (см., например, замечание к задаче 161078). Поэтому

(n – 1)n(n + 1)(n + 2) = (n² – 1)(n² + 2n) = (n² – 1)((n + 1)² – 1) = (n(n + 1) – 1)² – 1.

Ответ задачи отсутствует