Задача
Дан квадрат со
Решение
Обозначим через M0 исходный квадрат, M1 , M2 , M3 , ... – многоугольники, получаемые из M0 последовательным отрезанием уголков. Удобно рассмотреть также многоугольник Nk , вершинами которого служат середины сторон Mk ( k=0, 1, 2, ... )
Пусть A – произвольная вершина многоугольника Mk – а B и C – соседние с ней вершины. Чтобы получить из многоугольника Mk многоугольник Mk+1, нужно от каждой вершины A многоугольника Mk отрезать треугольник B2 AC2 (см.рис.8) такой, что точки B2 и 2 делит, соответственно, отрезки [AB] и [AC] в отношении 1:2. Пусть B1 и C1 – середины отрезков [AB] и [AC], т.е. соседние вершины многоугольника Nk ; тогда
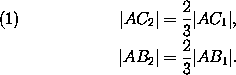
При переходе от многоугольника Nk к многоугольнику Nk+1 точки B1 и C1 остаются его вершинами, по уже не соседними: между ними появляется новая вершина A1 – середина отрезка [B2 C2]. Таким образом, многоугольник Nk+1 получается из многоугольника Nk добавлением к каждой его стороне [B1 C1] треугольника типа B1 A1 C1 .
Из(eq:234.1) следует, что площади отрезаемых и добавляемых треугольников связаны такими соотношениями:
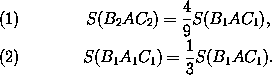
Пусть xk – площадь многоугольника Nk , yk – площадь Mk . Просуммировав(eq:234.2) и(eq:234.3) по всем вершинам A многоугольника Mk , получим:
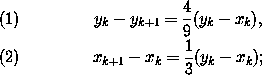
отсюда
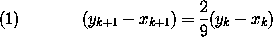
и

Отметим точки x0 , x1 , x2 , ... и y0 , y1 , y2 ,
... на числовой оси (рис.9 и10). Из соотношения(eq:234.6) следует,
что длина отрезка [xk+1,yk+1] в 4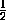 раза меньше длины
отрезка [xk,yk]. Рассмотрим точку a , делящую отрезок [xk,yk]
в отношении 3:4; тогда
раза меньше длины
отрезка [xk,yk]. Рассмотрим точку a , делящую отрезок [xk,yk]
в отношении 3:4; тогда

Учитывая(eq:234.7) и(eq:234.8), получим, что
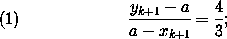
значит, точка a делит и том же отношении 3:4 и отрезок
Возьмем самый первый отрезок нашей последовательности: [x0,y0]=[
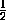 ,1]; в отношении 3:4 его делит точка a , такая, что
,1]; в отношении 3:4 его делит точка a , такая, что
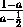 =
=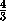 , т.е.
, т.е.

В силу сказанного, эта точка делит в отношении 3:4 все отрезки [xk,yk]
( k=0, 1, 2, ... ); значит, каждый следующий отрезок последовательности
[xk,yk] получается из предыдущего сжатием к точке a в 4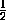 раза. Таким образом, точка a является единственной общей точкой всех
этих отрезков. (Можно выписать и точные формулы для xk и yk : xk=
раза. Таким образом, точка a является единственной общей точкой всех
этих отрезков. (Можно выписать и точные формулы для xk и yk : xk=
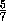 -(
-(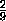 )k
)k 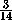 , yk=
, yk=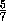 +
(
+
(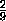 )k
)k 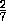 ; но нам они понадобятся. Читатели,
знакомые с понятием предела последовательности, конечно, заметили,
что a является общим пределом последовательностей xk и yk ; по
существу мы именно это и доказали.) Отсюда уже следует, что площадь искомой
фигуры M (являющейся пересечением всех многоугольников Mk ) равна a ;
действительно, M содержится в любом Mk и содержит любой Nk
(докажите (Это чисто теоретико-множественный факт: если Mk
; но нам они понадобятся. Читатели,
знакомые с понятием предела последовательности, конечно, заметили,
что a является общим пределом последовательностей xk и yk ; по
существу мы именно это и доказали.) Отсюда уже следует, что площадь искомой
фигуры M (являющейся пересечением всех многоугольников Mk ) равна a ;
действительно, M содержится в любом Mk и содержит любой Nk
(докажите (Это чисто теоретико-множественный факт: если Mk  Mk+1
Mk+1  Nk+1
Nk+1  Nk для каждого k=0, 1, 2, ... , и
M=k Mk , то M
Nk для каждого k=0, 1, 2, ... , и
M=k Mk , то M  Nk .) !); следовательно, площадь M
должна быть заключена между xk и yk (при всех k ), а этому требованию
удовлетворяет единственное число: a=
Nk .) !); следовательно, площадь M
должна быть заключена между xk и yk (при всех k ), а этому требованию
удовлетворяет единственное число: a=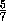 .
.
Можно было бы решать эту задачу и не вводя многоугольников Nk , используя
лишь соотношение, определяющее последовательность y0=1, y1=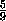 ,
y2 , y3 , ... :
,
y2 , y3 , ... :
yk-yk+1=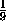 (yk-yk-1).
(yk-yk-1).
А.Зеленский (г.Шахтерск) обобщил задачу M234 на тот случай, когда
от каждой стороны отсекаются отрезки, составляющие  этой
стороны, где p – любое число, большее 2. Площадь получающейся в таком
случае фигуры равна
этой
стороны, где p – любое число, большее 2. Площадь получающейся в таком
случае фигуры равна 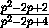 ; при p=3 получаем
ответ
; при p=3 получаем
ответ 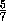 .
.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь