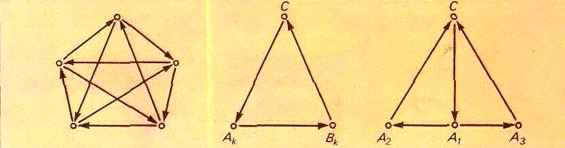
Индукция по n. База. При  n = 5  требуемый граф представлен на рис. слева.

  Шаг индукции. Рассмотрим  n + 1  точку. Пусть n из них уже соединены – получился граф с n вершинами. Можно считать, что каждые две из этих n точек соединены стрелкой: иначе проведём все недостающие стрелки (направив их в любую сторону), условие тем более будет выполняться. Обозначим (n+1)-ю точку через C и рассмотрим два случая.

  1)nчётно. Разобьёмnточек на пары. Пусть  {A_k, B_k}  – одна из пар  (1 ≤k ≤ ⁿ/₂)  и изA_kидёт стрелка вB_k. Тогда проведём изCстрелку вA_kи изB_kпроведём стрелку вC(рис. в центре). Так проделаем для каждой пары. Новый граф с  n+ 1  вершиной построен. ПустьX, Y– две любые различные его вершины.   Если иXиYне совпадают сC, то изXвYможно пройти (не более чем за два «хода») по индукционному предположению.   ПустьXилиYсовпадает сC. Тогда другая из этих точек (YилиX) входит в какую-то пару из тех, на которые мы разбили первыеnточек. Таким образом,XиY– это какие-то две из трёх точек, изображенных на центральном рисунке. Глядя на этот рисунок, легко перебрать все возможные варианты и убедиться, что требование выполняется.   2)nнечётно. Выберем любую вершинуA₁. Она соединена стрелками со всеми остальными вершинами:A₂, ...,A_n. ИзA₁выходят не менее чем две стрелки или вA₁входят не менее чем две стрелки (так как  n> 4).   Пусть изA₁выходят не менее чем две стрелки (второй случай аналогичен) – в вершиныA₂,A₃. Остальные вершины разобьем на пары. Теперь соединим стрелками новую вершину с тройкойA₁,A₂,A₃– как показано на рис. справа, а со всеми парами – как показано на рис. в центре. Как и в случае а), легко доказать, что полученный граф удовлетворяет условию задачи.

Ответ задачи отсутствует