Будем придерживаться следующих обозначений: большая жирная буква (например, X) обозначает треугольник, большие и маленькие буквы с индексами 1, 2, 3 (X₁, X₂, X₃, x₁, x₂, x₃) – вершины и противоположные им стороны этого треугольника (причём маленькие буквы обозначают также и прямые, на которых лежат стороны: X₂X₃ – прямая x₁, X₃X₁ – прямая x₂, X₁X₂ – прямая x₃.

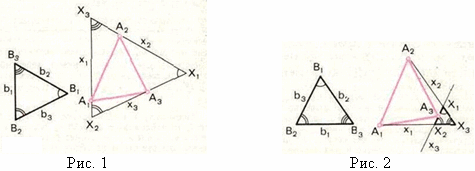
  Пусть треугольник B как угодно расположен в плоскости треугольника A. Проведём через вершины A₁, A₂ и A₃ прямые x₁, x₂, x₃, соответственно параллельные прямым b₁, b₂ и b₃. Ясно, что треугольники X и B подобны, поскольку стороны их соответственно параллельны (см. рис. 1 и 2).

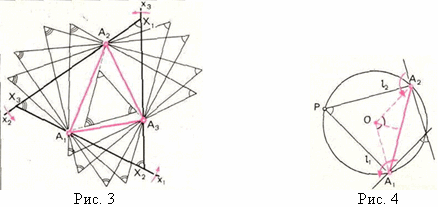
  Таким образом, мы построили треугольникX, подобный треугольникуB, стороны которого или их продолжения проходят через вершиныA₁,A₂,A₃треугольникаA.   Если вращать одновременно с одной и той же угловой скоростью прямуюx₁вокруг её точкиA₁,x₂– вокругA₂иx₃– вокругA₃, то мы получим целое семейство треугольниковX. Все это семейство мы обозначим буквойS. Ясно, что каждый треугольникXсемействаSподобенB. На рис. 3 видно, как меняется треугольникXпри повороте прямыхx₁,x₂,x₃; не очень ясно только, что происходит в "критический" момент, когда треугольникXстановится совсем маленьким; мы увидим, что в некоторый момент прямыеx₁,x₂,x₃проходят через одну точку, так что треугольникXвырождается в эту точку; затем прямыеx₁,x₂,x₃приближаются к своим первоначальным положениям (это происходит, когда каждая из них повернётся на угол π).  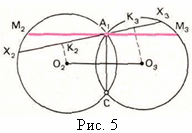Выясним более точно, как устроено семействоS. Заметим, что, когда две прямые равномерно вращаются вокруг двух своих точекA₁иA₂(рис. 4), точка их пересеченияPописывает окружность с центромO, для которого  ∠OA₁A₂= ∠OA₂A₁=^π/₂– φ, где φ – постоянный угол между прямыми, 0 ≤ φ ≤^π/₂.   При этом для точекPпо одну сторону от прямойA₁A₂уголA₁PA₂равен φ, а по другую –  π – φ.  Отсюда следует, что каждая из точекX₁,X₂,X₃– вершин треугольниковX – описывает окружности. Центры этих окружностей обозначим черезO₁,O₂,O₃(окружность с центромO₁проходит черезA₂иA₃и т.д.).   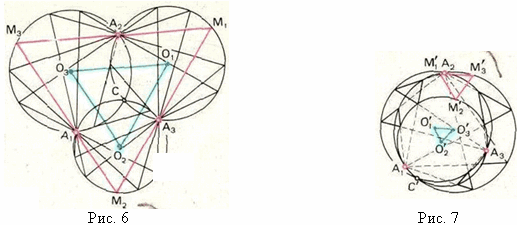Найдём теперь треугольник наибольшей площади. Воспользуемся тем, что все треугольникиXподобны, то есть и площадь, и длина каждой стороны максимальна у одного и того же из них. Рассмотрим, например, как меняется длина стороныX₂X₃(рис. 5). Поскольку окружности, по которым пробегаютX₂иX₃, обе проходят через точкуA₁, то основанияK₂иK₃перпендикуляровO₂K₂иO₃K₃, опущенных на прямуюx₁, – середины отрезковA₁X₂иA₁X₃. Поэтому  X₂X₃= 2K₂K₃.  Но длинаK₂K₃проекции отрезкаO₂O₃на прямуюx₁максимальна, тогда, когда  x₁||O₂O₃.  Разумеется, точно так же у этого треугольника  x₂||O₁O₂, x₃||O₂O₁. Отсюда ясно, как построить этот треугольникM.  Минимальный треугольник семействаSполучается, когда прямыеx₁,x₂,x₃перпендикулярны линиям центров соответствующих пар окружностей:O₂O₃,O₃O₁,O₁O₂; при этом все стороны треугольникаXравны нулю. Таким образом, все три вершины треугольникаXсовпадают – он вырождается в точку, обозначим еёC. Через эту точкуCпроходят все три окружности. Рисовать семейства треугольников видаSпроще всего, начиная именно с окружностей: если взять произвольно три окружности, проходящие через одну точкуC, обозначить отличные отCточки их попарного пересечения черезA₁,A₂,A₃, то можно принять любую точку на окружности за одну из трёх вершин треугольникаX, стороны которого проходят через точкиA₁,A₂,A₃, а вершины лежат на наших окружностях. Заметим ещё, что при гомотетии с центром в точкеCи коэффициентом 2 центры окружностейO₁,O₂,O₃переходят в вершиныM₁,M₂,M₃максимального треугольнике семействаS(рис. 6). Таким образом, треугольникOвсегда подобенB(возможен случай, когда треугольникOвырождается в точку и все три окружности совпадают).  Мы указали выше, какой именно треугольник семействаSнаибольший. Но это ещё не полностью решает задачу. Дело в том, что множество треугольников, подобныхBи описанных вокругA, не исчерпывается одним семействомS. Например, треугольникXна рис. 2 не входит в семействоS, порождённое треугольникомBрис. 1. Вообще, если отразить треугольникBотносительно какой-либо прямой (безразлично какой) и, исходя из полученного треугольникаB', построить семействоS'треугольников, – так же, как вначале мы строили семействоS, исходя изB, – то семействаSиS'не будут содержать общих треугольников. (Окружности, связанные с семействомS', получаются из окружностей, связанных сS, симметрией относительно прямыхa_i, см. рис. 7.) Таким образом, нужно найти наибольший треугольник в каждом из них и из этих двух треугольников выбрать больший.   Оказывается, однако, что можно сразу сказать, в каком из двух семействSиS'наибольший треугольник больше. 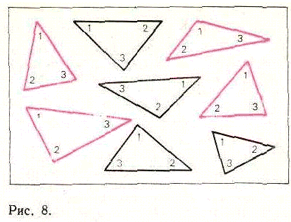Чтобы сделать это, а также чтобы разобраться, все ли нужные треугольники "охвачены" двумя семействамиSиS', воспользуемся ориентацией треугольников. На рис. 8 черные треугольники ориентированы по часовой стрелке, красные – против. Ясно, что все треугольники семействаSимеют одну ориентацию, а все треугольникиS'– противоположную. Можно доказать, что наибольший треугольник принадлежит семейству, ориентация которого совпадает с ориентациейA.  Теперь обсудим вопрос о том, все ли треугольники, описанные вокругAи подобныеB, мы изучили. Пока что мы рассмотрели все треугольники такого вида, получающиеся изBповоротом, гомотетией и, быть может, еще симметрией относительно прямой. Это всевозможные треугольникиX, которые подобныBс сохранением нумерации вершин, то есть так, что  ∠X₁= ∠B₁,  ∠X₂= ∠B₂,  ∠X₃= ∠B₃.  Итак, если требовать в условии именно такого подобия (то есть подразумевать, что  ∠M₁= ∠B₁,  ∠M₂= ∠B₂,  ∠M₃= ∠B₁,  то решение можно считать законченным: все множество допустимых треугольниковXисчерпывается двумя семействамиSиS', которые мы изучали.   Если же допускать подобия с "перенумерацией вершин" (то есть такие, что  ∠X₁= ∠B_i,  ∠X₂= ∠B_j,  ∠X₃= ∠B_k,  где  (i, j, k)  – любая перестановка из цифр 1, 2, 3), то получится не два, а 12 семействS_ijkиS'_ijk. Вершины треугольников из этих семейств заполнят 18 окружностей. (ЕслиBравносторонний, то семейств два; еслиBравнобедренный, то шесть.) На рис. 9а или 9б можно выбрать любую тройку прямых, попарно не параллельных и проходящих (по одной) через точкиA₁,A₂,A₃– обозначить их соответственноx₁,x₂,x₃– и получится один из представителей семействаS_ijkилиS'_ijk(при этом  x₁||b_i,  x₂||b_j,  x₃||b_k).  Оказывается, что и из этих 12 семейств можно указать то, в котором наибольший треугольник больше, чем во всех других. Чтобы сформулировать результат, условимся обозначать вершины треугольниковAиBтак, что ∠A₁≤ ∠A₂≤ ∠A₃  и  ∠B₁≥ ∠B₂≥ ∠B₃  (теперь мы можем это себе позволить), и расположим треугольникBтак, чтобы ориентацииAиBсовпадали. Тогда самый большой треугольник принадлежит семействуS₁₂₃.

Ответ задачи отсутствует