Задача
а) На рисунке слева изображены шесть точек, которые лежат по три на четырёх прямых. Докажите, что можно 24 разными способами отобразить это множество из шести точек на себя так, чтобы каждые три точки, лежащие на одной прямой, отобразились в три точки, лежащие на одной прямой.
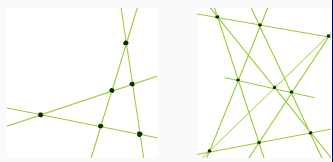
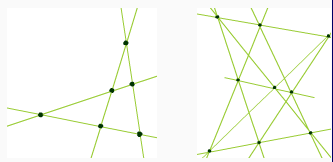
Решение
а) Если для каждой из наших четырёх прямых будет указано, на какую прямую она отображается, то тем самым определится и образ каждой точки (каждая точка нашей конфигурации является точкой пересечения определенных двух входящих в конфигурацию прямых). Множество из четырёх прямых можно отобразить на себя 4! = 24 способами. б) Отметим одну из прямых конфигурации l. Обозначим три лежащие на ней точки конфигурации A, B и C. Через эти точки проходят еще шесть прямых конфигурации. Остаются еще две прямые p и q, которые не проходят ни через одну из точек A, B и C.
Отобразим прямую l на какую-либо из девяти прямых конфигурации – на прямую l1. Выбрать её можно девятью способами. Точки A, B и C придётся отобразить на точки A1, B1 и C1, лежащие на прямой l1. Это можно сделать шестью способами. Прямые p и q должны отобразиться на две прямые p1 и q1, не проходящие через точки A1, B1, C1. Это можно сделать двумя способами. После этого образы остальных точек и прямых конфигурации будут однозначно определены.
Всего, таким образом, получится 9·6·2 = 108 отображений. в) Выберем одну из десяти прямых l. На ней расположены три точки A, B, C. Отличные от l прямые конфигурации, проходящие через точки A и B, пересекаются попарно еще в двух точках конфигурации X и Y. Отображение конфигурации на себя полностью определится, если задать образ l1 прямой l, образы A1, B1, C1 точек A, B, C, лежащие на прямой l1 и образы X1 и Y1 точек X и Y, которые должны быть точками попарного пересечения отличных от l1 прямых конфигурации, проходящих через точки A1 и B1. Всего получается 10·6·2 = 120 интересующих нас отображений.
Ответ
б) 108; в) 120 способами.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь