а) Предположим, что после отмены некоторых рейсов "связность" нарушилась. Рассмотрим некоторый город A, множество M всех городов, в которые можно проехать из A (возможно, с пересадками) и его дополнение N. Ясно, что между городами из M и N авиалиний нет. При этом в одном из этих множеств не более n городов; пусть их k.

  Первоначально каждый из этих городов был связан авиалиниями не менее чем с n городами, поэтому по крайней мере n + 1 – k  рейсов соединяли его с городами "чужого множества" и, следовательно, были отменены. Значит, всего было отменено не меньше чем  k(n + 1 – k)  рейсов. Но  k(n + 1 – k) > n – 1  при  k = 1, 2, ..., n .  Следовательно, если отменить  n – 1  рейс, то "связность" не нарушается.   б) Заметим, что  k(n + 1 – k) = n  лишь при  k = 1  и  k = n.  Если  k = 1,  то это значит, что некоторый город был связан рейсами ровно с n городами и все эти рейсы были отменены. Если  k = n,  то это значит, что некоторые n городов A₁, A₂, ..., A_n попарно соединены авиалиниями, оставшиеся n городов B₁, B₂, ..., B_n тоже попарно соединены авиалиниями и есть еще n рейсов, соединяющих города A₁ и B₁, A₂ и B₂, ..., A_n и B_n. На рисунке см. схемы авиалиний для  n = 2  и  n = 3.

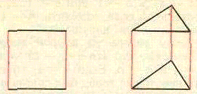
Ответ задачи отсутствует