Докажем, что кайму ширины 2 при  n = 4k + 1  можно обойти конем.

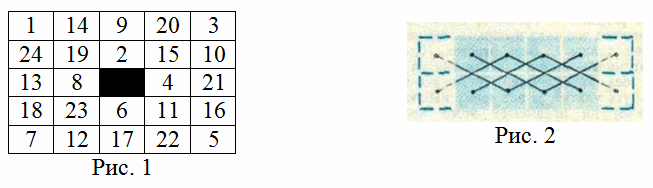
  На рис. 1 показано, как обойти кайму при  k = 0  (n = 1).

  Вставляя последовательно по четыре блока 2×4, изображённых на рис. 2, можно получить нужный обход при любомk(дляk= 1  такое построение приведено на рис. 3).   Лемма. Если в множестве G, состоящем из g полейбесконечной шахматной доски, можно выделить p попарно не пересекающихся подмножеств A₁, A₂, ..., A_k, которые содержат m полей, причём

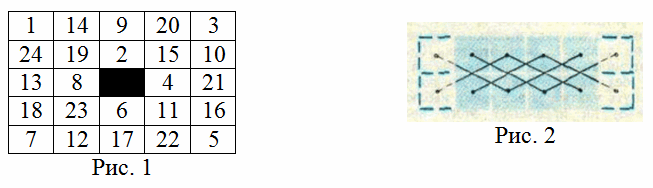
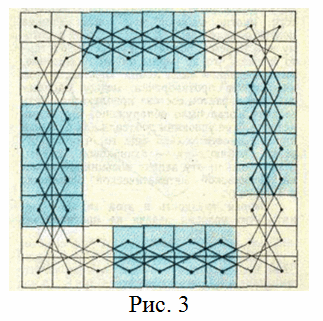
  а) ни с одного поля подмножества A_i конь не может пройти ни на одно поле подмножества A_j при  i ≠ j;

  б)  g – m < p – 1,&nbsp то область G нельзя обойти ходом коня.

  Доказательство. Если конём удастся обойти всё множество G, то путь коня должен пройти через все p подмножеств. При этом в силу условия а) при переходе из подмножества в подмножество коню придется не менее чем  p – 1  раз побывать нейтральных полях (не входящих ни в одно из подмножеств). Но таких полей по условию б) меньше  p – 1 .   Теперь докажем, что при  n ≠ 4k + 1  кайму обойти нельзя. Рассмотрим три случая.

  1)  n = 4k + 3.  При  k = 0  разделим всю кайму на два подмножества A₁ и A₂ так, как показано на рис. 4.

  Легко видеть, что из подмножестваA₁нельзя попасть в подмножествоA₂ходом коня. Поэтому можно применить лемму приp= 2, m = g.   Для того, чтобы получить рисунок при другихk, нужно вставлять блоки, изображённые на рис. 2.   2)  n= 4k.  При  k> 0  нейтральными объявим поля, имеющие по одной общей стороне с угловыми полями окаймляемой доски (на рис. 5 они помечены буквойZ). Их будет 8. Подмножества – их будет 10 – определяются следующим образом: берём незанятое поле и все те поля, в которые можно "пройти" из него конём, не пользуясь нейтральными клетками. Для того, чтобы из рис. 5, где  k= 1,  получить рисунок при любом  k> 0,  нужно вставлять блоки, изображённые на рис. 2.  При  k= 0  нейтральные поля и подмножества изображены на рис. 6.   3)  n= 4k+ 2.  Этот случай разбирается аналогично. Здесь при  k> 0  число нейтральных полей 12, а число подмножеств 14. Как выбирать нейтральные поля при  k> 0  и при  k= 0,  видно из рис. 7 и 8.

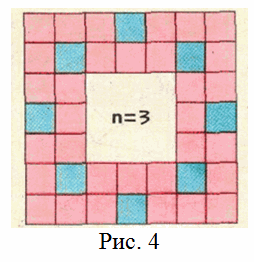
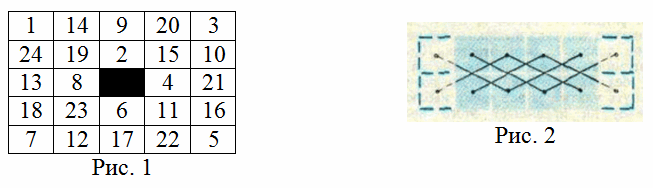
Ответ задачи отсутствует