Таблицы, удовлетворяющие условию задачи, образуют линейное пространство.

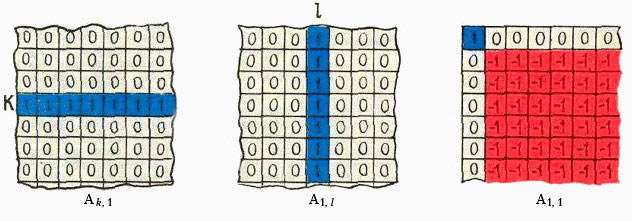
  Укажем  n + m – 1  линейно независимых таблиц: таблицы A_k1  (k = 2, 3, ..., m),  где k-я строка заполнена единицами, а остальные элементы равны нулю; таблицы A_il  (l = 2, 3, ..., n – 1),  где l-й столбец заполнен единицами, а остальные элементы равны нулю, и таблица A₁₁, у которой  a₁₁ = 1,  a_1j = 0,  a_i1 = 0  при  i, j > 1  и  a_ij = –1  при  i, j > 1  (см. рис.).

  Пусть числа, стоящие в некоторыхsклетках, определяют таблицу однозначно. Заметим, что только у нулевой таблицы в указанныхsклетках стоят нули. Действительно, если бы нашлась ненулевая таблицаB, у которой в нашихsклетках стояли бы нули, то было бы можно восстановить не только некоторую таблицуA, но и таблицу  A + B.   Докажем, что любые  s+ 1  таблиц  A₁,A₂, ...,A_s+1  линейно зависимы. Рассмотрим наборы чисел, стоящих в этих таблицах на указанных местах, как векторыa_iвs-мерном пространстве. Поскольку их  s+ 1,  то они линейно зависимы, то есть найдутся такие числа  λ₁, λ₂, ..., λ_s+1,  не все равные нулю, что у таблицы  A= λ₁A₁+ λ₂A₂+ ... + λ_s+1A_s+1  во всех наших клетках стоят нули. Как показано выше,  A= 0.   Следовательно,  s ≥ n + m– 1.

Ответ задачи отсутствует